Percentages & Ratios Cheat Sheet
A ratio says how much of one thing there is compared to another thing.

There are 3 blue squares to 1 yellow square
Ratios can be shown in different ways:
| Use the “:” to separate the values: | 3 : 1 | |
| Or we can use the word “to”: | 3 to 1 | |
| Or write it like a fraction: | 31 |
A ratio can be scaled up:
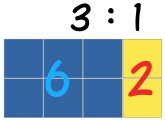
Here the ratio is also 3 blue squares to 1 yellow square,
even though there are more squares.
Using Ratios
The trick with ratios is to always multiply or divide the numbers by the same value.
Example:
4 : 5 is the same as 4×2 : 5×2 = 8 : 10 | 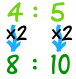 |
Recipes
Example: A Recipe for pancakes uses 3 cups of flour and 2 cups of milk.
So the ratio of flour to milk is 3 : 2
To make pancakes for a LOT of people we might need 4 times the quantity, so we multiply the numbers by 4:
3×4 : 2×4 = 12 : 8
In other words, 12 cups of flour and 8 cups of milk.
The ratio is still the same, so the pancakes should be just as yummy.
“Part-to-Part” and “Part-to-Whole” Ratios
The examples so far have been “part-to-part” (comparing one part to another part).
But a ratio can also show a part compared to the whole lot.
Example: There are 5 pups, 2 are boys, and 3 are girls

Part-to-Part:
The ratio of boys to girls is 2:3 or 2/3
The ratio of girls to boys is 3:2 or 3/2
Part-to-Whole:
The ratio of boys to all pups is 2:5 or 2/5
The ratio of girls to all pups is 3:5 or 3/5
Try It Yourself











Scaling
We can use ratios to scale drawings up or down (by multiplying or dividing).
The height to width ratio of the Indian Flag is 2:3 So for every 2 (inches, metres, whatever) of height |  |
If we made the flag 20 inches high, it should be 30 inches wide. If we made the flag 40 cm high, it should be 60 cm wide (which is still in the ratio 2:3) | |
Example: To draw a horse at 1/10th normal size, multiply all sizes by 1/10th
This horse in real life is 1500mm high and 2000 mm long, so the ratio of its height to length is
1500 : 2000
What is that ratio when we draw it at 1/10th normal size?
| 1500 : 2000 | = 1500×1/10 : 2000×1/10 | |
| = 150 : 200 |
We can make any reduction/enlargement we want that way.
Big Foot?
 | Allie measured her foot and it was 21cm long, and then she measured her Mother’s foot, and it was 24cm long. |
“I must have big feet, my foot is nearly as long as my Mum’s!”
But then she thought to measure heights, and found she is 133cm tall, and her Mum is 152cm tall.
In a table this is:
| Allie | Mom | |
| Length of Foot: | 21cm | 24cm |
| Height: | 133cm | 152cm |
The “foot-to-height” ratio in fraction style is:
| Allie: | 21133 | Mum: | 24152 |
So the ratio for Allie is 21 : 133
It is still the same ratio, right? Because we divided both numbers by the same amount.
And the ratio for Mum is 24 : 152
This time we divided by 8, but that ratio stays the same, too.
The simplified “foot-to-height” ratios are now:
| Allie: | 319 | Mum: | 319 |
“Oh!” she said, “the Ratios are the same”.
“So my foot is only as big as it should be for my height, and is not really too big.”
In calculating profit percent and loss percent we will learn about the basic concepts of profit and loss. We will recall facts and formula while calculating profit percent and loss percent. Now we will apply the concept of percentage to find profit/loss in selling and buying of goods in our day to day life.
Cost price (CP) The amount for which an article is bought is called its cost price.
Selling price (SP) The amount for which an article is sold is called its selling price.
Profit or gain When (SP) > (CP) then there is a gain.
Gain = (SP) – (CP)
Loss When (SP) < (CP) then there is a loss.
Loss = (CP) – (SP).
Notes:
The gain or loss is always reckoned on the cost price
Calculating Profit Percent and Loss Percent
Profit and loss formulas for calculating profit% and loss%:
I. Gain = (SP) – (CP)
II. Loss = (CP) – (SP)
III. Gain% = (gain / CP × 100)%
IV. Loss % = (loss/ CP × 100)%
V. To find SP when CP and gain% or loss% are given:
● SP = [(100 + gain %) / 100] × CP
● SP = {(100 – loss %) /100} × CP
VI. To find CP when SP and gain% or loss% are given:
● CP = {100/(100 + gain %)} × SP
● CP = {100 /(100 – loss %)} × SP
Calculating Profit Percent and Loss Percent
Worked-out problems on calculating profit percent and loss percent:
1. Mike bought a DVD for $ 750 and sold it for $ 875. Find Mike’s gain per cent.
Solution:
CP = $ 750 and SP = $ 875.
Since (SP) > (CP), Mike makes a gain.
Gain = $ (875 – 750)
= $ 125.
Gain% = {(gain/CP) × 100} %
= {(125/750) × 100} %
= (50/3) %
= 16 (2/3) %
2. Ron purchased a table for $ 1260 and due to some scratches on its top he had to sell it for $ 1197. Find his loss per cent.
Solution:
CP Rs.1260 and SP = $ 1197.
Since (SP) < (CP), Ron makes a loss.
Loss = $ (1260 – 1197)
= $ 63.
Loss % = [(loss / CP) × 100] %
= [(63 / 1260) × 100] %
= 5%
In calculating profit percent and loss percent, sometimes after purchasing an article, we have to pay some more money for things like transportation, repairing charges, local taxes, These extra expenses are called overheads.
For calculating the total cost price, we add overheads to the purchase price.
3. Maddy purchased an old scooter for $ 12000 and spent $ 2850 on its overhauling. Then, he sold it to his friend Sam for $ 13860. How much per cent did he gain or lose?
Solution:
Cost price of the scooter = $ 12000, overheads = $ 2850.
Total cost price = $ (12000 + 2850) = $ 14850.
Selling price = $ 13860.
Since (SP) < (CP), Maddy makes a loss.
Loss = $ (14850 – 13860) = $ 990.
Loss = [(loss / total CP) × 100] %
= [(990 / 14850) × 100] %
= 6
4. Ron ought an almirah for $ 6250 and spent $ 375 on its repairs. Then, he sold it for $ 6890. Find his gain or loss per cent.
Solution:
CP of the almirah = $ 6250,
Overheads = $ 375.
Total cost price = $ (6250 + 375)
= $ 6625.
Selling price = $ 6890.
Since, (SP) > (CP), Ron gains.
Gain% = $ (6890 – 6625)
= $ 265.
Gain% = [(gain / total CP) × 100] %
= [(265 / 6625) × 100] %
= 4 %
5. A vendor bought oranges at 20 for $ 56 and sold them at $ 35 per dozen. Find his gain or loss per cent.
Solution:
LCM of 20 and 12 = (4 × 5 × 3) = 60.
Let the number of oranges bought be 60.
CP of 20 oranges = $ 56
CP of 1 orange = $ (56 / 20)
CP of 60 oranges = $ [(56 / 20) × 60] = $ 168
SP of 12 oranges = $ 35
SP of 1 orange = $ [(35 / 12) × 60] = $ 175
Therefore, CP = $ 168 and SP = $ 175.
Since, (SP) > (CP), the vendor gains.
Gain = $ (175 – 168) = $ 7.
Gain % = [(gain / CP) × 100] %
= [(7 / 168) × 100] %
= 25 / 6 %
= 4 ¹/₆ %
6. If the cost price of 10 pens is equal to the selling price of 8 pens, find the gain or loss per cent.
Solution:
Let the cost price of each card be $ x
Then, CP of 8 pens = $ 8x.
SP of 8 pens = CP of 10 pens = $ 10x.
Thus, CP = $ 8x and SP = $ 10x.
Since, (SP) > (CP), there is a gain.
Gain = $ (10x – 8x) = $ 2x.
Gain % = [(gain / CP) × 100] %
= [(2x / 8x) × 100] %
= 25%
Comparing Old to New
 | Change: subtract old value from new value. Example: You had 5 books, but now have 7. The change is: 7-5 = 2. |
 | Percentage Change: show that change as a percent of the old value … so divide by the old value and make it a percentage: So the percentage change from 5 to 7 is: 2/5 = 0.4 = 40% |
Percentage Change is all about comparing old to new values. See percentage change, difference and error for other options.
How to Calculate
Here are two ways to calculate a percentage change, use the one you prefer:
Method 1
| Step 1: Calculate the change (subtract old value from the new value) |
| Step 2: Divide that change by the old value (you will get a decimal number) |
| Step 3: Convert that to a percentage (by multiplying by 100 and adding a “%” sign) |
| Note: when the new value is greater then the old value, it is a percentage increase, otherwise it is a decrease. |
Method 2
| Step 1: Divide the New Value by the Old Value (you will get a decimal number) |
| Step 2: Convert that to a percentage (by multiplying by 100 and adding a “%” sign) |
| Step 3: Subtract 100% from that |
| Note: when the result is positive it is a percentage increase, if negative, just remove the minus sign and call it a decrease. |
Examples
Example: A pair of socks went from $5 to $6, what is the percentage change?
Answer (Method 1):
- Step 1: $5 to $6 is a $1 increase
- Step 2: Divide by the old value: $1/$5 = 0.2
- Step 3: Convert 0.2 to percentage: 0.2×100 = 20% rise.
Answer (Method 2):
- Step 1: Divide new value by old value: $6/$5 = 1.2
- Step 2: Convert to percentage: 1.2×100 = 120% (i.e. $6 is 120% of $5)
- Step 3: Subtract 100%: 120% – 100% = 20%, and that means a 20% rise.

Another Example: There were 160 smarties in the box yesterday, but now there are 116, what is the percentage change?
Answer (Method 1): 160 to 116 is a decrease of 44. Compared to yesterday’s value: 44/160 = 0.275 = 27.5% decrease.
Answer (Method 2): Compare today’s value with yesterday’s value: 116/160 = 0.725 = 72.5%, so the new value is 72.5% of the old value.
Subtract 100% and you get -27.5%, or a 27.5% decrease.
Why Compare to Old Value?
Because you are saying how much a value has changed.
Example: Milk was $2, now it is $3, did it rise $1 compared to $2 or $3 ?
We compare to the original $2 value, so we say the change is $1/$2 = 0.5 which is a 50% increase.
The Formula
You can also put the values into this formula:
New Value − Old Value |Old Value| × 100%
(The “|” symbols mean absolute value, so negatives become positive)
Example: There were 200 customers yesterday, and 240 today:
240 − 200 |200| × 100% = 40 200 × 100% = 20%
A 20% increase.
Example: But if there were 240 customers yesterday, and 200 today we would get:
200 − 240 |240| × 100% = −40 240 × 100% = −16.6…%
A 16.6…% decrease.
How to Reverse a Rise or Fall
Some people think that a percentage increase can be “reversed” by the same percentage decrease. But no!
Example: 10% of 100
A 10% increase from 100 is an increase of 10, which equals 110 …
… but a 10% reduction from 110 is a reduction of 11 (10% of 110 is 11)
So we ended up at 99 (not the 100 we started with)
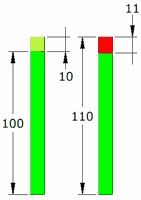
What happened?
- 10% took us up 10
- Then 10% took us down 11
Because the percentage rise or fall is in relation to the old value:
- The 10% increase was applied to 100
- But the 10% decrease was applied to 110
How to do it properly
To “reverse” a percentage rise or fall, use the right formula here:
| To Reverse: | Use this Percent: | Example 10% |
|---|---|---|
| An “x” percent rise: | x/(1+x/100) | 10/(1+10/100) = 10/(1.1) = 9.0909… |
| An “x” percent fall: | x/(1-x/100) | 10/(1-10/100) = 10/(0.9) = 11.111… |
| Percent Rise: <=> Percent Fall: |

